EXPLICACIÓN:
1) Factorizo los denominadores:
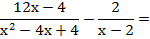
Primera fracción:
x2 - 4x + 4 = (x - 2)2 con el
Tercer Caso: Trinomio
Cuadrado Perfecto
x
-2
2.x.(-2)
-4x
Segunda fracción:
x - 2 no se puede factorizar por ningún Caso (los
que no se pueden factorizar)
Ahora reemplazo el denominador que factoricé, por su equivalente factorizado. Va quedando así:
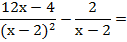
2) El denominador común: Mínimo Común Múltiplo
Como en la suma de fracciones numéricas, si los denominadores son diferentes, hay que
buscar un denominador común. Que debe ser el Mínimo Común Múltiplo (m.c.m)
entre los denominadores de todas las fracciones. Una explicación completa
de cómo calcular el m.c.m. entre polinomios, con variedad de ejemplos se puede
ver aquí: M.C.M. ENTRE
POLINOMIOS.
Aquí explicaré lo que creo necesario para que se entienda en este ejemplo en
particular:
Denominadores:
(x - 2)2
(x - 2)
Hay un solo factor:
(x - 2)
Con el mayor exponente con que aparecen:
(x - 2)2
En el denominador de la primera fracción
m.c.m: (x + 2)2
(El m.c.m. es: "Es el producto (multiplicación) de todos los
factores, con el
mayor exponente con el que aparecen") M.C.M.
Bajo una sola línea de fracción pongo el denominador común, el m.c.m. que
encontré, y en el siguiente paso (paso 3) determinaré lo que queda en el
numerador:
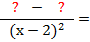
3) El numerador:
Una vez determinado el denominador común, hay que seguir el mismo procedimiento
que para la suma de fracciones numéricas: Se divide a éste por los denominadores de cada fracción, y se
multiplica el resultado por el numerador de la fracción correspondiente (ver
ejemplo con fracciones numéricas):
Pongamos aquí los dos pasos anteriores, para que se vean los numeradores que
teníamos y el denominador común:
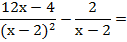
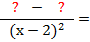
Primera fracción:
Divido el denominador común por el denominador de
la primera fracción:
(x - 2)2 dividido (x - 2)2, es igual a 1
(divisiones)
Luego, multiplico ese resultado por el numerador de la primera fracción:
1.(12x - 4)
Me va quedando:
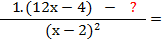
Segunda fracción:
Divido el denominador común por el denominador de
la segunda fracción:
(x - 2)2 dividido (x - 2), es igual a (x - 2) (divisiones)
Luego, multiplico ese resultado por el numerador de la segunda fracción:
(x - 2).2, que es igual a 2.(x - 2)
Me queda:
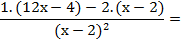
4) Operar en el numerador para llegar a la mínima expresión:
Lo más complicado ya pasó. Ahora nos queda "trabajar" en el
numerador: distributiva, juntar términos de igual grado, etc. Lo hago aquí
fuera de la fracción, para que se distinga más lo que estoy haciendo en este
paso:
1.(12x - 4) - 2.(x - 2) = 12x - 4 - 2x + 4 = 10x
Me quedó:
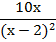
Como 10x no se puede factorizar por ningún Caso, ése es el resultado final.
¿Te quedó alguna duda? Preguntáme en el
LIBRO
DE CONSULTAS
CONCEPTOS - DUDAS - COMENTARIOS
Los Conceptos Generales de este tema están en: SUMA Y RESTA
Explicación de las divisiones que se hicieron en este ejemplo:
Como ya expliqué con más detalles en otro apartado (ver
aquí), hacer estas divisiones es lo mismo que
simplificar una fracción, ya que una fracción representa a la división entre
su numerador y su denominador.
Resolver (x - 2)2 dividido (x - 2)2, sería lo mismo
que simplificar la fracción:
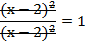 (SIMPLIFICACIÓN DE
EXPRESIONES ALGEBRAICAS RACIONALES)
(SIMPLIFICACIÓN DE
EXPRESIONES ALGEBRAICAS RACIONALES)
Resolver (x - 2)2 dividido (x - 2), sería lo mismo que simplificar la
fracción:
1
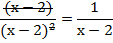 (¿por qué si
simplifica así?)
(¿por qué si
simplifica así?)
Puede observarse que lo que sucede es que se cancelan los polinomios que son
iguales. Teniendo en cuenta esto, se pueden resolver mentalmente estas divisiones, pensando
en que algunos de cancelan y otros quedan. Así:
"Si divido a (x - 2)2 dividido (x - 2)2, se me va a cancelar
todo, y me queda 1 como resultado.
"Si divido a
(x - 2)2 dividido (x - 2), se me va a
cancelar un (x - 2), y me queda como resultado un (x - 2)"
Observación: El denominador común "incluye" a todos los
denominadores. Divisibilidad entre polinomios factorizados.
Como dije en el EJEMPLO 3, voy a mostrar cómo siempre denominadores de cada fracción están "incluidos" en el
denominador común. Eso es lo mismo que decir que en el m.c.m. están incluidos
los polinomios entre los cuales estoy buscando el m.c.m.
En este EJEMPLO 6:
Para que se vea dónde el denominador 1 está incluido en el denominador común,
lo marcaré en rojo:
Denominador 1: (x - 2)2
Denominador común: (x - 2)2
Para que se vea dónde el denominador 2 está incluido en el denominador común,
lo marcaré en azul:
Denominador 2: (x - 2)
Denominador común: (x - 2)2 = (x - 2).(x - 2)
En los siguientes ejemplos seguiré mostrando que en el m.c.m. están
"incluidos" todos los denominadores. Y es porque el m.c.m. es
justamente un producto de factores que incluya a todos los denominadores, pero
que use la menor cantidad de factores posibles. Y eso es porque el denominador
común tiene que ser divisible por todos los denominadores. A veces, darse cuenta de
eso puede servir para encontrar el denominador común sin pensar en la regla
para obtener el m.c.m.
Para más información, conceptos y ejemplos resueltos,
consultar en:
SUMAS Y RESTAS DE EXPRESIONES ALGEBRAICAS RACIONALES
Explicaciones de otros ejemplos:
EJEMPLO 1 (Suma de fracciones con igual denominador)
EJEMPLO 2 (Resta de fracciones con igual denominador)
EJEMPLO 3 (Con distintos denominadores)
EJEMPLO 4 (Con denominadores factorizables)
EJEMPLO 5
EJEMPLO 7 (Con tres términos)
EJEMPLO 8 (Uno de los factores es un número)
EJEMPLO 9 (Con números como factores)
EJEMPLO 10 (Uno de los factores es la x)
EJEMPLO 11 (La x como factor, a distintas
potencias)
EJEMPLO 12 (Uno de los términos es un entero)
EJEMPLO 13 (En los denominadores hay un solo término)
EJEMPLO 14 (Se puede simplificar antes de sumar
las fracciones)
Política de Privacidad - Contacto:
matematicaylisto@gmail.com