DIFERENCIA DE CUADRADOS / EXPLICACIÓN DEL EJEMPLO 8

EJEMPLO 8: (Con la resta "al revés")

-x² + 4 = 4 - x² = (2 + x).(2 - x)

             2    x

El primer término es negativo y el segundo es positivo. Pero puedo escribirlos "al revés", y ahí tengo la resta de cuadrados que necesito.

EXPLICACIÓN:


1) Primero cambio el orden de los términos, para que quede como una resta de dos cuadrados, que es la forma que tiene que tener un polinomio para poder aplicar este Caso. Queda entonces.

4 - x²           Aquí tengo dos cuadrados restándose: 4 y x²


2) Las bases son entonces: 2 y x


3) El resultado de la factorización es entonces:

(2 + x).(2 - x)           SUMA POR RESTA DE LAS BASES

CONCEPTOS - DUDAS - COMENTARIOS

Los conceptos generales del caso están en CONCEPTOS - DIFERENCIA DE CUADRADOS


¿Qué tiene de particular este ejemplo?

Que tal como está dado el polinomio (-x² + 4), no parece una resta de dos cuadrados. Porque el primer término es el negativo y el segundo es positivo. Pero se puede cambiar el orden de los términos, ya que -x² + 4 es igual a 4 - x². Así, se ve que es una resta de dos cuadrados: El 4 restando a x². Ese cambio de orden se puede hacer por la Propiedad Conmutativa de la Suma.


No entiendo la aplicación de la Propiedad Conmutativa de la Suma en este ejemplo

La Propiedad Conmutativa dice que, para cualquier número Real:

a + b = b + a

Como a y b son números reales, pueden ser números positivos o negativos
(¿qué es un número real?). Es decir que esta propiedad vale tanto para números positivos o negativos. En nuestro ejemplo:

-x² + 4  es una suma de dos números: -x² sumado a 4  (¡¿-x² es un número?!)

Si aplicamos la Propiedad Conmutativa, podemos decir que ese polinomio es igual a:

4 + (-x²)    Ya que la propiedad nos autoriza a escribir la suma al revés.

Pero si saco el paréntesis (reglas para sacar paréntesis), me queda:

4 - x²


Verificación de la factorización:

Aplico la Propiedad Distributiva en el resultado:  (¿Cómo se hacen estas "Distributivas"?)

(2 + x).(2 - x) = 4 - 2x + 2x - x² = 4 - x². Que como dijimos antes, es igual a -x² + 4


¡¿-x² es un número?!

Las letras de las expresiones matemáticas representan a números. Se ponen letras en lugar de números, porque esas letras pueden ser reemplazadas por distintos números, para obtener un valor de esa expresión, según el número que se le ponga. Por ejemplo:

-x² + 4    Vale -3² + 4, si se reemplaza la x con el número 3. Lo cual dá -9 + 4, es decir: -5
              Pero vale -(-1)² + 4, si se reemplaza la x con el número -1. Lo cual dá -1 + 4 = 3

Así, se puede reemplazar la x por cualquier número, y se obtienen distintos valores para el Polinomio. Es lo que algunos le llaman "Valor Numérico" de un polinomio. 

De manera que podemos tratar a -x² como si fuera un número, aplicarle las propiedades de los números, trabajar con -x² como si fuera un número. Porque "tarde o temprano va a ser un  número", ya que el sentido de las expresiones con letras es que las letras sean reemplazadas alguna vez con números. 
Aprendemos a trabajar con estas expresiones algebraicas (polinomios), para saber qué hacer con las "fórmulas", que tienen letras cuyo valor puede variar ("variables"). Pensemos en las otras Ciencias, que usan fórmulas relacionadas con el mundo real. En esas fórmulas, hay letras que de seguro van a ser reemplazadas con números. Por eso es necesario aprender en Matemática lo que se puede hacer con esas fórmulas.


¿Qué es un número "real"?

Primero que nada: ¿Por qué estoy hablando de los números reales? Porque la Propiedad Conmutativa de la Suma que mencioné, es válida para todo el Conjunto de los Números Reales. Por lo demás, no tiene nada que ver con este tema de los Polinomios y este Caso de Factoreo ni este ejemplo.

"Reales" es el nombre de un conjunto. Así como "Naturales", "Enteros", "Racionales", etc. El conjunto de los Números Reales incluye a casi todos los números con los que trabajamos en Matemática:

- Los números Naturales: 1, 2, 3, 4, 5, 6, etc (hasta el infinito)
- Los números Enteros: 0, -1, -2, -3, -4, etc (hasta el infinito) y todos los Naturales.
- Los números Racionales: Las fracciones y los números Decimales Exactos y Periódicos. Por ejemplo: 1/2; 5/3; 0,04; 15,37; 0,1333333333... ó 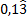; etc. Y también incluye a todos los Naturales y Enteros.
- Los números Irracionales: Los números decimales con infinitas cifras decimales que no son periódicas. Por ejemplo: 2,345678910111213..., 0,1122334455667788991010111212...  Eso incluye a las raíces "no exactas" (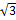 = 1,732050808...; 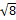= 2,28427125...). Y números famosos como PI (3,1415926535897) y e (2,718281828459045....).

Todos esos números forman el Conjunto de los Números Reales, y son los que "llenan" la recta numérica. En realidad, debido a que algunos de los conjuntos que nombré se incluyen unos en otros, podríamos resumir al Conjunto de los Reales como la Unión de los siguientes dos Conjuntos: Racionales e Irracionales.
¿Cuáles números no son Reales? Por ejemplo, los Números Complejos. Son esos números que tienen la "i", y que se aprenden en los últimos años del Nivel Medio. Por ejemplo: 2 + 3i ; -5i; etc.


Otros ejercicios resueltos, parecidos al Ejemplo 8:

-16 + x² = x² -16 = (x + 4).(x - 4)

               x     4


- 4/9 + a⁶ = a⁶ - 4/9 = (a³ + 2/3).(a³ - 2/3)

                  a³   2/3


-b⁸ + 2,25 = 2,25 - b⁸ = (1,5 + b⁴).(1,5 - b⁴)

                  1,5     b⁴


- 81 + y⁴ = y⁴ - 81 = (y² + 9).(y² - 9)

                 y²    9




Para más información, conceptos y ejemplos resueltos, consultar en:
QUINTO CASO: DIFERENCIA DE CUADRADOS


Explicaciones de otros ejemplos:

EJEMPLO 1 (Fácil)
EJEMPLO 2 (Con dos letras)
EJEMPLO 3 (Con el número "1")
EJEMPLO 4 (Con fracciones)
EJEMPLO 5 (Con potencias distintas de 2)
EJEMPLO 6 (Con términos compuestos)
EJEMPLO 7 (Con números decimales)
EJEMPLO 9 (Uno "con todo")
EJEMPLO 10 (Normalizar un polinomio)

Política de Privacidad - Contacto: matematicaylisto@gmail.com